Unidad 1

FUNCIONES, LÍMITES Y CONTINUIDAD

1.1 Las Funciones.

Se presenta el concepto de función, definiendo los elementos que conforman una función: El dominio, el conjunto de llegada y la regla. Se explican los conceptos de rango, imagen. Se presentan ejemplos de relaciones de la vida real que son funciones y otros ejemplos que no son funciones.

- Funciones reales de variable real: La definición es presentada en el video. También se verá el significado de variable independiente y dependiente. ¿Cómo se puede presentar la definición de una función? Al final del video se explica la notación funcional de funciones. Se usa esta notación para representar los valores de la función.

- Evaluación de funciones: El proceso de evaluación de funciones para determinar el valor de la función en un valor se realiza con muchísima frecuencia. En el video se puntualiza como evaluar funciones, no sólo en valores numéricos sino en expresiones algebraicas, dando consejos a fin de minimizar los errores que suelen cometer algunos estudiantes en este tipo de cálculo.

- Dominio implícito (natural): En el video se explica el dominio implícito de una función y cómo determinarlo cuando la función está definida a través de una fórmula algebraica sencilla.

Otros cuatro videos muy importante para afianzar aun mas los conceptos sobre Dominio y Rango de una función, son los siguientes:

a. - Dominio de una Función: Se presenta el concepto de dominio de una función y cómo hallar el dominio en diferentes funciones de variable real. Se explican tres casos especiales de funciones: la función racional, las funciones con raíces pares y las funciones con logaritmos.

b. - Dominio de funciones más complicadas: En el video anterior se definieron nuevas funciones a partir de funciones conocidas y se discutió la definición del dominio de las nuevas funciones, más complicadas. Esta discusión servirá para analizar como determinar el dominio de funciones más complicadas a las ya vistas. En el video se presenta este enfoque para determinar el dominio de funciones que pueden ser interpretadas como suma, diferencia, producto o cociente de expresiones.

c. - Rango de una Función: Concepto de rango de una función de variable real y cómo hallar el rango de una función con distintos ejemplos Las consideraciones vistas para el dominio son similares pero para hallar el rango es necesario expresar a x en términos de la variable dependiente y.

d. - Video de ejercicios planteados: Es de mucha importancia que veas este video para afianzar los conocimientos sobre cómo encontrar el dominio de una función.

- Gráfica de una función: La gráfica de una función ayuda a interpretar mejor las relaciones entre las variables. Aquí veremos una técnica para gráficas de funciones, obteniendo algunos puntos mediante una tabla de valores, representándolos en el plano y uniendo los puntos con un trazo suave. Se presenta en el video la definición de la gráfica de una función. La gráfica de una función no es otra cosa que la gráfica de la ecuación y=f(x). Entre todas las técnicas existentes para graficar, en el video se recordará la técnica punto a punto. Se insistirá en la necesidad de conocer el dominio de la función como primer paso para obtener la gráfica de la función con esta técnica. Se obtendrá la gráfica de la función raíz de x.

- Operaciones algebraicas con funciones: Nuevas funciones surgen cuando sumamos, restamos o multiplicamos funciones conocidas. Se da la definición de nuevas funciones obtenidas a través de las cuatros operaciones elementales, considerando el dominio.

- Función compuesta: Dada dos funciones podíamos obtener nuevas funciones combinándolas con las operaciones las básicas de suma, diferencia, producto y cociente. También podremos obtener nuevas funciones realizando la composición de funciones. En el video se presenta la definición de la función compuesta y se desarrollan varios ejemplos en que se determinan funciones compuestas, dando recomendaciones de trabajo.

- Función Inversa: Se ha estudiado cuando una ecuación en x y y define a y como función de x. Esa misma ecuación puede definir a x como función de y. En este caso tenemos la función inversa de la primera. No toda función definida a través de una ecuación tiene función inversa. El concepto de función uno a uno (biunívoca, inyectiva) es clave para definir la función inversa de una función dada.

Se establece el criterio o prueba de la recta horizontal para determinar si la función es o no uno a uno.

Se propone una sucesión de pasos para obtener la inversa. La gráfica de la función inversa de f puede ser obtenidad a partir de la gráfica de la función f reflejando esta última en la recta.

- Cómo obtener una función inversa: Se recomiendan una serie de pasos para obtener la función inversa de una función dada. Se desarrolla un ejemplo para obtener la función inversa de una función dada siguiendo los pasos recomendados.

- Gráfica de una función inversa: Recuerde que la gráfica de la función y=f (x+c) puede ser obtenida a partir de la gráfica de f. La cuestión ahora es Si f tiene función inversa, ¿se puede obtener la gráfica de la función inversa a partir de la gráfica de f ? Un ejemplo es resuelto paso a paso dando recomendaciones de trabajo.

- Algunas funciones elementales: función definida por partes, función cuadrática o potencial, exponencial y logarítmica.

- Teoría y ejercicios sobre Funciones exponenciales.

- Teoría y ejercicios sobre Funciones Logarítmicas.

- Funciones trigonométricas: Las funciones trigonométricas son funciones cuyos valores son extensiones del concepto de razón trigonométrica en un triángulo rectángulo trazado en una circunferencia unitaria (de radio unidad). Definiciones más modernas las describen como series infinitas o como la solución de ciertas ecuaciones diferenciales, permitiendo su extensión a valores positivos y negativos, e incluso a números complejos.

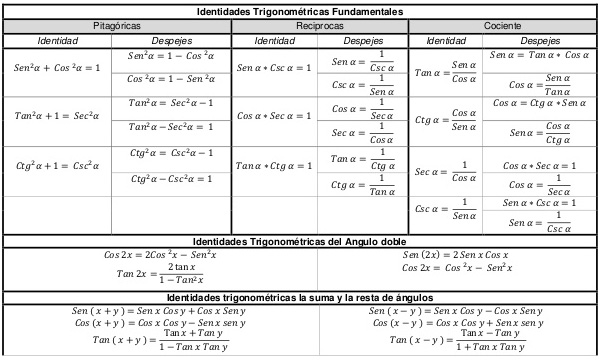
Aquí te dejo unos apuntes que te servirán de apoyo sobre Trigonometría.

Toda esta teoría está muy bien explicada tanto en los videos que las acompañan como en el capítulo correspondiente al libro El Cálculo de Louis Leithold sobre "Funciones".

- A continuación te dejo la Guía de Ejercicios Nr. 1 sobre Funciones, tomados del libro de Cálculo de Louis Leithold indicado en la Bibliografía: Guía de Ejercicios Nr. 1 . Igualmente te agrego las soluciones de los ejercicios de la Unidad 1 del libro correspondiente: Solucionario de ejercicios de la Unidad 1 del libro Cálculo de Louis Leithold.

- LÍMITES.

1.2 Límites por definición.

- Concepto intuitivo: En este video se da una introducción al concepto de límite de una función de variable real usando como método de cálculo la evaluación directa de los valores cercanos a x en la función. Incluso se ilustra que el límite de una función para un x que tiende a un número dado no necesariamente coincide con evaluar la función en ese valor. (cortesía del canal de youtube "Mas Aprendo")

Concepto intuitivo de Límites.

- Concepto formal: En este video se muestra la definición formal de límite que usa epsilon y delta enunciada por primera vez por el matemático Cauchy. Se explican los elementos que componen dicha definición a través de un ejemplo numérico.

Seguidamente se muestra otra explicación sencilla y ejemplo de un Límite por Definición. 
Igualmente les presento un segundo ejemplo de resolución de un límite por definición: Ejemplo 2.

- Propiedades y teoremas sobre límites: En este video se enuncian, sin demostrar, las propiedades generales de los límites tal como se acostumbra en los cursos regulares de cálculo (límite de la suma y resta de funciones, límite del cociente y producto de funciones, límite del producto de una constante y una función, límite de una constante, límite de una potencia y una raíz) . Pero en este caso se hace con el fin de mostrar la propiedad más importante de todas, y es que el límite de una función en punto cualquiera "a" donde "a" hace parte del dominio de la función es precisamente el valor de la función evaluada en dicho punto, lo cual sirve para encontrar la gran mayoría de límites que se presentan en cálculo. Lim x tiende a "a" de f(x) es igual a f(a) siempre que "a" pertenezca al dominio de f(x).

- A continuación te dejo la Guía de Ejercicios Nr. 2 sobre Definición y Propiedades de los Límites, tomados del libro de Cálculo de Louis Leithold indicado en la Bibliografía.

- Ejemplos del cálculo del Límite de una función: En este video se ilustra con tres ejemplos de distinta naturaleza como encontrar el límite de una función de variable real.

a. El primer ejemplo nos muestra un caso donde a través de factorización podemos eliminar una indeterminación de la forma cero dividido cero y encontrar el límite.

b. El segundo ejemplo nos muestra el caso donde el límite no existe cuando llegamos a una división de un número entre cero.

c. El tercer ejemplo nos muestra como eliminar una indeterminación igual a la del primer ejemplo pero a través de racionalización

- Límites laterales: Explicación de como calcular los límites laterales de una función (límite por la derecha y por la izquierda). ¿Cómo encontrar los límites laterales de una función?¿Qué es un límite lateral? En este video se ilustra con un ejemplo qué es un límite lateral. Si nos piden calcular el límite de una función cuando X tiende a un límite lateral (en el video ejemplificamos con 1 por la derecha o 1+, lo que quiere decir dar valores a la función cercanos a 1 pero mayores que él).

1.3 Límites determinados para funciones.

- Límites determinados para funciones:

  a. Polinómicas y racionales.

  b. Radicales. 

  c. Trigonométricas: Para resolver los límites de funciones trigonométricas, es IMPRESCINDIBLE conocer a fondo los principios de trigonometría, sus valores principales, sus teoremas, sus identidades; solo así podrás resolver estos límites. A continuación te presento un ejemplo donde se aplican identidades trigonométricas  y otro ejemplo sobre sustitución de variables y teoremas de límites para este tipo de funciones.  Le agrego un tercer ejercicio con sustitución de variables y teorema de límites de funciones trigonométricas.

  d. Exponenciales.

  e. Logarítmicas.

- Límites determinados infinitos.

- Límites en el infinito.

a. Conceptos básicos de límites al infinito. Se muestran las operaciones básicas de suma, resta, multiplicación y división donde se encuentra involucrado el infinito y los números reales. Se trata de explicar en que casos dichas operaciones pueden realizarse y cuando aparecen indeterminaciones.

b. Se ilustra los casos en que es posible eliminar las indeterminaciones del tipo infinito sobre infinito mediante la división de la función racional por la "x" de mayor potencia. Se ilustra el procedimiento para encontrar la mayor potencia en funciones que contienen raíces.

c. Solución de límites al infinito cuando se tienen indeterminaciones del tipo infinito menos infinito mediant el uso de racionalización. Solución de problemas donde el límite tiende a infinito negativo.

1.4 Límites indeterminados.

- 0 / 0:

a. En este primer video se muestran dos ejemplos resueltos de como calcular un límite indeterminado usando para ambos casos la diferencia de cuadrados para factorizar y de esta forma eliminar la indeterminación.

b. En este segundo video se muestra un ejemplo resuelto de como calcular un límite indeterminado usando la regla de ruffini para factorizar el numerador y denominador de la función analizada y de esta forma eliminar la indeterminación.

c. En este tercer video se muestra un ejemplo resuelto de como calcular un límite indeterminado usando tanteo para factorizar el numerador y diferencia de cuadrados para el denominador de la función analizada y de esta forma eliminar la indeterminación.

d. En este cuarto video se muestra un ejemplo resuelto de como calcular un límite indeterminado con una suma de fracciones que se convierte en una indeterminación del tipo 0/0 la cual luego se elimina tras factorizar el numerador en este caso.

e. En este quinto video se muestra un ejemplo resuelto de como calcular un límite indeterminado con una suma de fracciones que se convierte en una indeterminación del tipo 0/0 la cual luego se elimina tras efectuar una división simple entre un elemento del denominador y numerador de la fracción resultante.

- ∞/∞; +∞ ; -∞

- A continuación te dejo la Guía de Ejercicios Nr. 3 sobre Evaluación de los Límites.

1.5 Cálculo de Asíntotas de una curva.

a. Horizontales, verticales: Procedimiento para encontrar asíntotas verticales y horizontales en una función racional mediante el uso de límites.

b. Oblicuas.

1.6 Continuidad y discontinuidad.

- Definiciones de Continuidad y discontinuidad de funciones en un punto o en un conjunto.
- Tipos de discontinuidad.
a. Concepto intuitivo de continuidad y discontinuidad de una función mostrando ejemplos gráficos que ilustran cuando la discontinuidad es removible. Concepto formal (matemático) de continuidad de una función mediante el uso de límites. Se listan las condiciones necesarias para que exista continuidad en un punto.
b. Se muestra como aplicar el concepto de continuidad de una función en un punto para una función a tramos analizando precisamente el valor de x donde la función cambia. En el videos se hace especial énfasis en usar límites laterales para garantizar la existencia del límite (se aclara el hecho de que si el límite existe y hay una discontinuidad esta es removible).
c. Se muestra un ejemplo típico de una función a tramos a donde se desconoce un parámetro y debe hallarse para que la función sea continua. El procedimiento es estándar y consiste en tomar el límite de la función por derecha y por izquierda en el punto o puntos donde la función a tramos varía y se igualan para poder resolver el valor del parámetro. Si la función tiene imagen igual al límite se da por terminado el problema, de lo contrario se debe redefinir la función.

BIBLIOGRAFÍA Y RECURSOS:
- Louis Leithold (1998). El Cálculo, Séptima Edición; Edición Oxford University Press, Mexico.ISBN: 0-673-46913-1.
- Louis Leithold (1998). Solucionario de los ejercicios de la Unidad 1 del libro El Cálculo, Séptima Edición.
- Academia online Unicoos.com  http://www.unicoos.com
- Matemáticatuya.com: http://www.matematicatuya.com/FUNCIONES/
- Blog de Cálculo del profesor (Colombia) Julio Rios Gallego: http://julioprofe.net/courses_group/calculo/
- Graficadora de Funciones OnLine EXPERYMENTE

Recuerda que ya no estás en el Liceo;
"PIENSA Y COMPÓRTATE" ...

COMO UN PROFESIONAL.